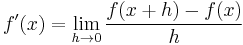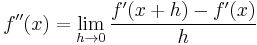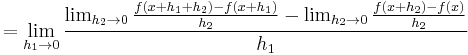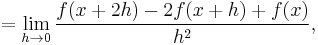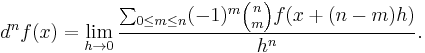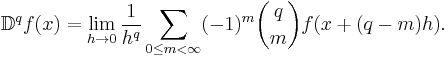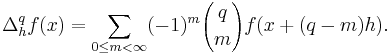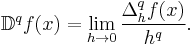Grünwald–Letnikov derivative

In mathematics, the Grünwald–Letnikov derivative is a basic extension of the derivative in fractional calculus, that allows one to take the derivative a non-integer number of times. It was introduced by Anton Karl Grünwald (1838–1920) from Prague, in 1867, and by Aleksey Vasilievich Letnikov (1837-1888) in Moscow in 1868.

Constructing the Grünwald–Letnikov derivative

The formula

f'(x) = \lim_{h \to 0} \frac{f(x%2Bh)-f(x)}{h}

for the derivative can be applied recursively to get higher-order derivatives. For example, the second-order derivative would be:

f''(x) = \lim_{h \to 0} \frac{f'(x%2Bh)-f'(x)}{h}
= \lim_{h_1 \to 0} \frac{\lim_{h_2 \to 0} \frac{f(x%2Bh_1%2Bh_2)-f(x%2Bh_1)}{h_2}-\lim_{h_2 \to 0} \frac{f(x%2Bh_2)-f(x)}{h_2}}{h_1}

Assuming that the h 's converge synchronously, this simplifies to:

= \lim_{h \to 0} \frac{f(x%2B2h)-2f(x%2Bh)%2Bf(x)}{h^2},

which can be justified rigorously by the mean value theorem. In general, we have (see binomial coefficient):

d^n f(x) = \lim_{h \to 0} \frac{\sum_{0 \le m \le n}(-1)^m {n \choose m}f(x%2B(n-m)h)}{h^n}.

Formally, removing the restriction that n be a positive integer, it is reasonable to define:

\mathbb{D}^q f(x) = \lim_{h \to 0} \frac{1}{h^q}\sum_{0 \le m < \infty}(-1)^m {q \choose m}f(x%2B(q-m)h).

This defines the Grünwald–Letnikov derivative.

Another notation

We may also write the expression more simply if we make the substitution:

\Delta^q_h f(x) = \sum_{0 \le m < \infty}(-1)^m {q \choose m}f(x%2B(q-m)h).

This results in the expression:

\mathbb{D}^q f(x) = \lim_{h \to 0}\frac{\Delta^q_h f(x)}{h^q}.

References